What is the Acid Test?

To most geologists, the term "acid test" means placing a drop of dilute (5% to 10%) hydrochloric acid on a rock or mineral and watching for bubbles of carbon dioxide gas to be released. The bubbles signal the presence of carbonate minerals such as calcite, dolomite, or one of the minerals listed in Table 1.

The bubbling release of carbon dioxide gas can be so weak that you need a hand lens to observe single bubbles slowly growing in the drop of hydrochloric acid - or so vigorous that a flash of effervescence is produced. These variations in effervescence vigor are a result of the type of carbonate minerals present, the amount of carbonate present, the particle size of the carbonate, and the temperature of the acid.

Magnesite: The mineral magnesite, which has a chemical composition of MgCO₃, will effervesce weakly with warm hydrochloric acid and very weakly with cold acid. Specimen is about 6.4 cm across.

What Causes the Fizz?

Carbonate minerals are unstable in contact with hydrochloric acid. When acid begins to effervesce (fizz) on a specimen, a reaction similar to the one shown below is taking place.

On the left side of this reaction, the mineral calcite (CaCO₃) is in contact with hydrochloric acid (HCl). These react to form carbon dioxide gas (CO₂), water (H₂O), dissolved calcium (Ca⁺⁺), and dissolved chlorine (Cl^--). The carbon dioxide bubbles that you observe are evidence that the reaction is taking place. When that occurs, calcite or another carbonate mineral is present.

Many other carbonate minerals react with hydrochloric acid. Each of these minerals consists of one or more metal ions combined with a carbonate ion (CO₃^--). The chemistry of these reactions is similar to the calcite reaction above. The mineral reacts with hydrochloric acid to produce carbon dioxide gas, water, a dissolved metal ion, and dissolved chlorine. The reactions for magnesite (MgCO₃) and siderite (FeCO₃) are shown below.

Calcite: This transparent specimen of calcite shows cleavage that is characteristic of the mineral. Calcite, with a composition of CaCO₃, will react strongly with either cold or warm hydrochloric acid. Specimen measures about 10 cm across.

Acid Reactions of Carbonate Minerals
Mineral	Chemical Composition	Cold Acid Reaction	Warm Acid Reaction
Aragonite	CaCO3	strong	strong
Azurite	Cu3(CO3)2(OH)2	yes	strong
Calcite	CaCO3	strong	strong
Dolomite	CaMg(CO3)2	weak	yes
Magnesite	MgCO3	very weak	weak
Malachite	Cu2CO3(OH)2	yes	yes
Rhodochrosite	MnCO3	weak	yes
Siderite	FeCO3	very weak	weak
Smithsonite	ZnCO3	weak	yes
Strontianite	SrCO3	yes	yes
Witherite	BaCO3	weak	weak
Table 1: A list of commonly and occasionally encountered carbonate minerals with their chemical formula and reactions to cold and warm hydrochloric acid. Test results can vary because of weathering, previous testing, contamination, and specimen purity.

The Vigor of Carbonate Reactions

Careful observation is important because some carbonate minerals react vigorously and others barely react with cold acid.

The carbonate mineral that is most commonly encountered by geologists is calcite (CaCO₃). Calcite is a "ubiquitous" mineral. Ubiquitous means "found everywhere." Calcite occurs in igneous, metamorphic, and sedimentary rocks and is the most commonly encountered carbonate mineral. If you place one drop of cold hydrochloric acid on calcite, the entire drop of acid will erupt with bubbles and a vigorous fizz will last for a few seconds.

Dolomite CaMg(CO₃)₂ is another commonly encountered carbonate mineral. If you place one drop of cold hydrochloric acid on a piece of dolomite, the reaction is weak or not observed. Instead of seeing an obvious fizz, you will see a drop of acid on the surface of the mineral that might have a few bubbles of carbon dioxide gas slowly growing on the dolomite surface.

However, if warm acid is placed on dolomite, an obvious fizz will occur. This occurs because the acid and rock react more vigorously at higher temperatures.

If you place a drop of hydrochloric acid on powdered dolomite, a visible reaction will occur. This is because the surface area has been increased, making more dolomite available to the acid. (You can easily make dolomite powder by scratching a specimen of dolomite across a streak plate. Then test the powder by placing a drop of hydrochloric acid on the powder. Another easy way to produce a small amount of mineral powder is to scratch the specimen with a nail.)

Different carbonate minerals have different responses to hydrochloric acid. A list of common and occasionally encountered carbonate minerals is given in Table 1 with their chemical composition and their relative reaction with cold and warm hydrochloric acid.

When a mineral has a weak response to acid, you must be observant and patient to see it. For example, magnesite has a very weak reaction with cold HCl. If you powder a small amount of magnesite on a streak plate and place a drop of acid on it, you might not see any action for several seconds. Then, as tiny bubbles begin to form on particles of magnesite, the drop of acid will appear to grow larger in size. That occurs as carbon dioxide is liberated from the mineral and displaces the water. Observing the formation of bubbles with a hand lens can be helpful.

Dolostone: Dolostone is a sedimentary rock composed primarily of the mineral dolomite, which has a chemical composition of CaMg(CO₃)₂. Dolomite will effervesce weakly with cold hydrochloric acid, producing a few bubbles. The reaction is more noticeable when the acid is warm and/or the stone is powdered. The specimen in the photo is about 10 cm across.

The Acid Test on Rocks

LIMESTONE, DOLOSTONE, AND MARBLE

Some rocks contain carbonate minerals, and the acid test can be used to help identify them. Limestone is composed almost entirely of calcite and will produce a vigorous fizz with a drop of hydrochloric acid. Dolostone is a rock composed of almost entirely of dolomite. It will produce a very weak fizz when a drop of cold hydrochloric acid is placed upon it, a more obvious fizz when powdered dolostone is tested, and a stronger fizz when hot hydrochloric acid is used.

Limestone and dolostone can be a little more complex. They are sometimes composed of a mixture of calcite and dolomite and have acid reactions that are deceptive. A dolostone can contain enough calcite to fool you into calling it a limestone. For these rocks the acid test might not be enough for a confident identification - but at least you will know that the rock has a significant carbonate mineral content.

Marble is a limestone or a dolostone that has been metamorphosed. It will have an acid reaction that is similar to the limestone or dolostone from which it was formed.

Other Applications of the "Acid Test": Geologists can use dilute hydrochloric acid to help identify the cementing agent of sandstones. They place a drop of dilute HCl on the sandstone and closely observe. If calcite is the cementing agent, an effervescence will occur and some of the sand grains might be liberated. A hand lens or small microscope is used to make the observations. The photo above is a magnified view of a piece of Oriskany Sandstone, an Ordovician-age rock unit from the Appalachian Basin that serves as a natural gas reservoir and a natural gas storage unit. Oriskany sandstone is often cemented by calcite.

OTHER ROCKS THAT FIZZ

Always remember that "calcite is ubiquitous." (Ubiquitous means that it is found almost everywhere.)

Many rocks contain small amounts of calcite or other carbonate minerals. All of these can produce a fizz even though the carbonate is only a minor part of a rock's composition. These rocks might contain small veins or crystals of carbonate minerals that produce a fizz in contact with acid. These veins and crystals can be so tiny that they are not visible to the unaided eye. This small amount of carbonate might fizz the first time a drop of acid is applied but be depleted and not fizz if acid is applied a second time to the same location on the rock.

Some sedimentary rocks are bound together with calcite or dolomite cement. Sandstone, siltstone, and conglomerate sometimes have calcite cement that will produce a vigorous fizz with cold hydrochloric acid. Some conglomerates and breccias contain clasts of carbonate rocks or minerals that react with acid.

Many shales were deposited in marine environments and contain enough calcium carbonate to produce a vigorous acid fizz. These shales were formed when mud was deposited in an environment similar to or adjacent to where limestone was formed. They are composed of sedimentary clay minerals intermixed with a small amount of calcite. They are known as "calcareous shales."

Don't allow an acid fizz to guide the identification process. In many cases it will instead add detail to your observation such as: "calcareous shale" or "sandstone with carbonate cement." This is valuable information.

Vinegar can be used for the acid test: Vinegar can be a safe, economical and easy-to-obtain "acid" for identifying calcite and dolomite. Vinegar is dilute acetic acid that produces a very weak reaction with calcite and dolomite - best observed with a hand lens.

The "Vinegar Test" Vinegar is a dilute acetic acid solution (about 5% to 10%) that produces a weak effervescent reaction with calcite and dolomite. It can be used instead of hydrochloric acid for introducing students to the acid test. Vinegar is easy to obtain, inexpensive, and safer to use than hydrochloric acid. The effervescence using vinegar usually requires a hand lens for clear observation and is only observable with carbonate minerals that have a strong reaction with hydrochloric acid. Vinegar is often used when the acid test is part of a precollege course. Protective gloves, glasses, paper towels, and immediate access to an eyewash station are recommended.

EXTREME ACID REACTIONS

A few rocks can produce an extreme reaction with hydrochloric acid. These are usually rocks composed of calcite or aragonite with abundant pore space or extremely high surface areas. Some specimens of chalk, coquina, oolite, and tufa are examples. When a drop of dilute hydrochloric acid is placed on these specimens, an eruption of acid foam can rise up off of the rock and spread to an unexpected diameter. The reaction is very brief (and may not be repeatable), but it is so sudden and vigorous that it can surprise an inexperienced person. This description is for one drop of acid. If more is used an even more vigorous reaction will occur. (These extreme reactions will not occur with every specimen of these rocks. Be aware when testing them or presenting them to students for testing.)

The extremely vigorous reaction of cold hydrochloric acid with these specimens occurs because the rocks are so porous or because they have a very high surface area under a single drop of acid.

TEST UNWEATHERED MATERIAL

Calcite and other carbonate minerals have a low resistance to weathering and can be attacked by acids in natural waters and soils. When testing material that has been exposed at Earth's surface, it is very important to test unweathered material. A fresh surface can usually be obtained by breaking the rock.

DECEIVED BY POROSITY!

Some rocks are porous and contain a reservoir of air. Small amounts of air escaping into a drop of acid from below can give the appearance of a gentle acid reaction. Don't be fooled. If you place a drop of acid on some sandstones, a few bubbles will emerge out of pore spaces. It's not a carbonate cement. To avoid this problem scratch the rock across a streak plate and test the powder or the grains that are produced.

The best way to learn about minerals is to study with a collection of small specimens that you can handle, examine, and observe their properties. Inexpensive mineral collections are available in the Geology.com Store. Image copyright iStockphoto / Anna Usova.

Contamination in Mineral Identification Labs

When students are given minerals to identify, two situations can cause problems with their work.

1) In mineral identification labs, some students are ready to call any mineral that produces an acid reaction "calcite" or another carbonate. However, calcite is a ubiquitous mineral and it is often present as an intimate part of other mineral specimens and rocks. These can produce a false acid reaction. To avoid being misled, students should always be cautioned to confirm a specimen's identity with multiple properties. If a specimen fizzes with acid but has a Mohs hardness of seven and breaks with a conchoidal fracture, then it certainly isn't calcite!

Depending upon the experience of the students, specimens that are very true to their properties can be presented to the class, or specimens with some challenges can be used. Lots of minerals found in the field will not be absolutely true to properties. It's better to learn that lesson in the lab and go into the field with wisdom.

2) Since calcite is one of the index minerals of the Mohs Hardness Scale, it is often used to test the hardness of mineral specimens. This can place small amounts of calcite potentially on every unknown specimen in the lab! Don't assume that a single acid reaction is correct. Test the specimen in a second location if you suspect that contamination has occurred.

In a mineral identification lab, barite is commonly confused with calcite because of contamination. The barite might naturally contain small amounts of calcite, or the hardness testing of a previous student might have left small amounts of calcite on a barite specimen. Students are often drawn to an identification as "calcite" simply because of the acid test. If that mineral exhibits a bit of cleavage and is not very hard, then many students will arrive at an incorrect identification.

Limiting Frivolous Acid Use in Labs

Most students are intrigued with the acid test and want to try it. To limit frivolous acid use, students should be instructed to use a single drop of acid for the test and to only test specimens when carbonate minerals are suspected. If that is not done, some students will use the acid frivolously. This behavior is encouraged if the classroom is equipped with large acid bottles that are filled to the top. However, if the acid bottles are small and nearly empty at the beginning of class, students usually ration their use of the acid to appropriate amounts. Small, nearly empty bottles makes less acid available to spill.

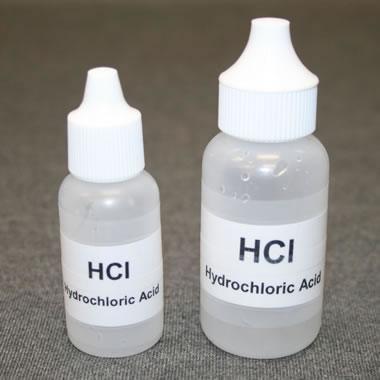
Acid dispensing bottles: Small acid dispensing bottles work well for the acid test. They dispense the acid one-drop-at-a-time and will not spill if they are knocked over. If you are a teacher supervising the acid test in a classroom, give students small bottles that are nearly empty. That will reduce the amount of frivolous acid use that might otherwise occur. Label the bottles clearly and instruct students in acid use before making them available.

Acid Bottle Selection

The type of bottle selected for dispensing the acid is important. Laboratory supply stores sell bottles that are designed for dispensing acid one-drop-at-a-time. The lid is always on these bottles (except when they are being cleaned or refilled), and they do not produce a spill when they are knocked over. Bottles with a removable lid that has a squeeze bulb dispenser will be occasionally knocked over when the lid is off if they are being used by normal humans.

Acid dispensing bottles should be made of rigid plastic with a small opening which allows acid to be easily dispensed one-drop-at-a-time. Soft dispensing bottles or bottles with a larger opening can dispense a large amount of acid with an accidental squeeze.

Sources of Hydrochloric Acid

Hydrochloric acid diluted to a 10% solution cannot be purchased in most communities. The best place to purchase commercially prepared solutions is from a laboratory supply company. Purchasing it ready-for-use is the recommended way to obtain it. Don't try to prepare your own solution if you don't know exactly what you are doing and have an equipped laboratory. Your chemistry department might be able to assist you with ordering acid. Some generous chemists will prepare a 10% solution for you.

Mineral Specimens as "Consumables"

Mineral specimens that are used properly in the science classroom or laboratory will need to be replaced frequently. Students will be investigating them with hardness tests, streak tests, acid tests and other experiments. All of these tests damage the specimen and make it less fit for the next group of students. To keep the acid test from fouling your entire collection, ask students to rinse specimens after testing with acid and limit testing to only when it is needed.